 LAS
OPERACIONES INTRAPROPOSICIONALES Y EL NÚMERO
LAS
OPERACIONES INTRAPROPOSICIONALES Y EL NÚMERO
José
Manuel Serrano González-Tejero
 Rosa María
Pons Parra
Rosa María
Pons Parra
 María José Serrano Quetglas
María José Serrano Quetglas
Universidad de Murcia (España)
INTRODUCCIÓN
Como dice Jean-Blaise Grize en sus Observaciones sobre la epistemología matemática de los números naturales, “hay muy pocas obras acerca de la epistemología del número que no citen la frase de Kronecker: Dios creó los números enteros; el resto es obra del hombre” (Grize, 1979; p. 109). Esta expresión, un tanto irónica si se quiere, denota una precisa concepción de las matemáticas: su aritmetización.
El proceso de aritmetización de las matemáticas requiere un análisis que aunque reposa de forma directa en los números reales, todos sabemos que estos entes han podido ser definidos, en el último cuarto del siglo XIX, a partir de los racionales. Sin embargo, todo número racional puede, y debe, ser entendido como pareja de números enteros, los cuales, a su vez, pueden ser concebidos en términos de pares de números naturales. De esta manera, los números naturales vienen a constituirse en la pieza esencial de todo el edificio aritmético. Es, por tanto, comprensible que, además de los esfuerzos propios de los matemáticos y epistemólogos de las matemáticas, las actividades de gran parte de los psicólogos y pedagogos de todo el mundo se haya centrado, y se continúe centrando, en la psicogénesis del número natural, con el fin de poder dar respuesta a una doble pregunta ¿en qué consisten estos entes, cuyo origen parece ser contemporáneo del hombre, y que, en la cultura actual, hemos designado como 1, 2, 3, ..., n? y, lo que es más importante para nosotros, ¿cómo son aprehendidos por el individuo?.
Con relación a la primera pregunta se suscita una cuestión de enorme importancia, pues si bien los matemáticos están bastante de acuerdo acerca de las propiedades formales de los números naturales, ya no lo están tanto respecto a la naturaleza de los mismos y, en este sentido, todas las teorías matemáticas (intuicionistas, empiristas o reduccionistas), incluso aquellas que se han venido mostrando como las más eficientes desde la perspectiva de un análisis metamatemático, vienen a recoger, de alguna manera, la polémica número cardinal – número ordinal que, partiendo de los pitagóricos, ha llegado hasta nuestros días.
En efecto, ya en el siglo VI a.C., los griegos distinguían entre dos tipos diferentes de números científicos:
a) Una composición de unidades con un origen común. Por ejemplo, la mónada es el principio de todos los unos, la díada el de los doses, la tríada el de los treses, etc., y
b) Un raudal de mónadas, lo que podría entenderse como un conjunto finito numerable.
Esto supone un hecho doble, de gran importancia a la hora de centrar los trabajos sobre la construcción del número natural. En primer lugar aparece el número con una identidad propia, es decir, cada número presenta un valor intrínseco y unas propiedades igualmente intrínsecas, que le confieren una personalidad independiente de la base de numeración (Ghyka, 1978) y, en segundo lugar, toma cuerpo la división que hace referencia a la doble cualidad de los números: su aspecto cardinal y ordinal, reflejado, respectivamente, en los dos tipos de números científicos de las matemáticas helénicas.
Por esta razón encontramos siempre, y en cualquier teoría sobre la construcción del número natural, dos ideas primarias que, habitualmente, no suelen ser definidas: clase y orden. Esas dos nociones básicas podrían ser descritas con una cierta exactitud de la siguiente manera:
orden es una relación de la forma A < B y que quiere decir que A precede a B o que B sucede a A.
clase es una relación de la forma A Ì B y que quiere decir que todos los A son algunos B.
A las ideas de clase y orden se asocian dos formas de cuantificación, una, vinculada al orden, recibe el nombre de ordenación y se define como la construcción de una relación cuantitativa asimétrica; la otra, asociada a las clases, recibe el nombre de cardinación y se basa en la construcción de relaciones simétricas.
Esta dualidad del número ha sido asumida por la Psicología, de manera que algunos investigadores reconocen como propiedad más sobresaliente de los números naturales su inherente ordenación, mientras que otros consideran que el rasgo más distintivo es la conjetura de que cada miembro de la serie de los números se puede concebir como una clase supraordenada que es la suma lógica de todas las clases subordinadas que contienen ese número determinado de elementos.
Los resultados de las investigaciones en este campo no parecen estar suficientemente claros y así, algunos autores identifican el origen psicológico del número con el origen psicológico del número ordinal (Brainerd, 1979; Kingma y Koops, 1981), puesto que mantienen que los números se refieren a los términos de las relaciones asimétricas transitivas y, por tanto, son recursos para representar los términos de las progresiones que dichas relaciones generan. En este sentido, las teorías psicológicas ordinalistas postulan que el hecho más destacable de los números es que, cualquiera que sea el símbolo verbal o escrito empleado, su propósito original es simplemente simbolizar el hecho del orden.
Por el contrario, otro conjunto de autores, más o menos veladamente, sostienen que el principio cardinal es más relevante que el ordinal en la construcción del número (Gelman y Gallistel, 1978), postura que parece estar avalada por algunos análisis históricos (Collette, 1985).
Finalmente, una teoría ad hoc parece querer salir del posible «impasse» que crean las posiciones cardinales y ordinales del número, y es la teoría de Jean Piaget, que partiendo de consideraciones psicológicas (particularmente evolutivo-cognitivas), por un lado, y de consideraciones matemáticas, por otro, intenta una reconciliación de las teorías cardinales y ordinales.
La teoría de Piaget sobre el número se basa en una acumulación no aditiva de las teorías de Frege-Russell y de Peano (Serrano, 1982; Smith, 2002), con la consideración del número como indisociablemente cardinal y ordinal y confiriéndole un carácter de sintético e irreductible. Como diría el propio Piaget, “es cierto que nuestra hipótesis permite, en cierto sentido, escapar de esta alternativa (intuicionismo, logicismo, aritmetización), pues si el número es clase y relación asimétrica al mismo tiempo, no deriva de tal o cual operación lógica (o aritmética) particular sino simplemente de la reunión de ellas, lo que concilia la continuidad con la irreductibilidad y conduce a concebir como recíprocas y no ya como unilaterales las relaciones entre la lógica y la aritmética” (Piaget y Szeminska, 1975; p. 11).
Es evidente que tomar partido por cualquiera de estas opciones supone condicionar todas las actividades conducentes a un proceso de enseñanza-aprendizaje para la adquisición de las nociones numéricas elementales. En efecto, partir de una postura ordinalista equivale a potenciar los esquemas de orden (seriación, conteo, etc.) en el desarrollo de actitudes numéricas, partir de una postura cardinalista supone, por el contrario, un potenciamiento de los esquemas cardinales (clasificación, correspondencia, etc.), partir de posiciones intuicionistas o empiristas nos conduciría a poner al sujeto en situaciones concretas tales que permitieran la “emergencia” de la intuición numérica, etc.
En este sentido, la posición piagetiana parece tener una mayor consistencia didáctica. En efecto, por un lado, cabe pensar que, en el intento de discretizar el universo a fin de asimilarlo, comprenderlo y conferirle un significado, el individuo organiza lo real clasificándolo y ordenándolo para poder establecer relaciones cuantitativas entre esto que ha sido cualificado y ordenado. Por otro lado, deja escaso margen de dudas el hecho de que el esquema de cuantificación más eficaz y, probablemente más eficiente, para la resolución de problemas aritméticos elementales es el esquema de conteo (Serrano y Denia, 1987; 1994). Ahora bien, el esquema de conteo supone la coordinación de esquemas cardinales y ordinales, puesto que contar es hacer corresponder unas palabras (numerales) a unos objetos, en un orden determinado. Definir el número, desde una perspectiva psicopedagógica supone, por tanto, hacer referencia a dos tipos de cuantificación, la cardinación y la ordenación, lo que viene avalado por los análisis ontogenético (Piaget y Szeminska, 1975), filogenético (Guitel, 1975) y formalizante (Serrano, 1982). En definitiva, podemos observar que la consideración del número como síntesis de relaciones de equivalencia (clasificación) y relaciones de orden (seriación) y las referencias a los trabajos de Jean Piaget, se manifiestan en la mayor parte de los trabajos actuales, siendo una preocupación común en los educadores de los primeros niveles educativos de todos los países (Becker, 1998; Ciancio, Sadovsky, Malabonga, Trueblood y Pasnak, 1999; Garret, Busby y Pasnak, 1999; Mareschal y Shultz, 1999; Planche, 1998; Van de Rijt y Van Luit, 1999).
MÉTODO.
A tenor de todo lo dicho podemos plantear nuestra hipótesis general de trabajo sobre la conceptualización del número:
H1: “Si el número es indisociablemente cardinal-ordinal, entonces el desarrollo de los esquemas de clase y orden determinarán materialmente su adquisición”.
1. Sujetos. La población hace referencia a los dos niveles superiores de Educación Infantil y a los dos primeros niveles de Educación Primaria (Primer Ciclo) del término municipal de Murcia (España). El número de unidades de que consta la mencionada población se sitúa en torno a los quince mil escolares. El tamaño muestral fue de 134 sujetos con un rango de edad de 49-102 meses (m = 75’15 y s = 14’84) con lo que el nivel de significación de nuestra muestra, aplicando el índice de Krejcie y Morgan (1970), es de a = 0’25 (c² = 1’352).
El tipo de muestreo empleado fue un muestreo aleatorio estratificado, considerando como estratos poblacionales los distintos niveles escolares (cuatro: 2º y 3º del segundo ciclo de Educación Infantil y el primer ciclo, 1º y 2º, de Educación Primaria), y como subestratos poblacionales los entornos donde se ubican los colegios (dos: rural y urbano). La distribución de los sujetos por estratos es la siguiente (la edad se expresa en meses):
Educación Infantil: Número de sujetos: 63; rango de edad (en meses): 49-74; m = 61,60 y s = 7’4.
a) 2º Ciclo-2º Curso: Número de sujetos: 35; rango de edad: 49-64; m = 55’91 y s = 3’84.
b) 2º Ciclo-3º Curso: Número de sujetos: 28; rango de edad: 60-74; m = 68’71 y s = 3’83.
Educación Primaria: Número de sujetos: 71; rango de edad: 75-102 (en meses); m = 87’18 y s = 7’65.
c) 1º Ciclo-1º Curso: Número de sujetos: 41; rango de edad: 75-89; m = 81’46 y s = 3’53.
d) 1º Ciclo-2º Curso: Número de sujetos: 30; rango de edad: 88-102; m = 95’00 y s = 3’91.
2. Procedimiento. En primer lugar se diseñó y elaboró el material y los protocolos de las cinco pruebas de que constaba la experiencia. Todas las pruebas fueron pasadas en los propios Centros, de forma individual, y en una dependencia habilitada especialmente para desarrollarlas. La duración de una sesión de trabajo con un alumno no excedía, en ningún caso, de los cuarenta y cinco minutos y este tiempo variaba en función del nivel cognitivo de los sujetos. Además, cuando el experimentador notaba cualquier signo de fatiga o aburrimiento en el niño, la sesión se daba por concluida.
Los experimentadores dialogaban, previamente, con los niños (en una especie de juego ajeno a las pruebas, pero con el material que se iba a utilizar) a fin de determinar su capacidad semántica y adaptar las consignas verbales a un lenguaje asequible y familiar para el niño. Todos los experimentadores estaban cualificados y habían sido adiestrados previamente en el contenido y metodología de las pruebas a través de una actividad de formación que duró ocho sesiones de una hora (aproximadamente).
Prueba de clasificación
Inicialmente se procedió a establecer una prueba que permitiera medir la variable denominada Clasificación. Las tareas utilizadas fueron similares a las descritas por Piaget e Inhelder (1975), pero añadiendo al material de bloques lógicos de Z.P. Dienes un material específico (soldados a caballo y a pie) que podía ser organizado como clase lógica o clase colectiva (Serrano y Fernández, 1989).
Los bloques lógicos utilizados constaban de tres tipos de figuras geométricas (cuadrados, triángulos y círculos) y tres colores distintos (azul, amarillo y rojo), existiendo siempre tres elementos idénticos desde la perspectiva de los dos criterios (forma x color).
Las consignas utilizadas variaban en función del nivel cognitivo de los sujetos y se elaboraban, de forma individual, en una fase previa a la presentación de la prueba, a través de una entrevista-juego con materiales diversos. En esta entrevista se trataba de averiguar la capacidad semántica del niño para organizar lo real desde el punto de vista de las clases. Las consignas más utilizadas fueron del tipo: “Pon juntos los que se parecen”, “pon juntos los que sean como éste”, etc.
Los niveles genéticos fueron establecidos a partir de las propiedades de las clases descritas por Piaget e Inhelder (1975; pp. 60-61).
En función de estas propiedades, y atendiendo a las conductas encontradas en el desarrollo de las clases, se establecieron siete niveles genéticos. Los dos primeros niveles pertenecen al estadio de las colecciones figurales y, el último, al de las clases. Los restantes niveles se adscriben al estadio de colecciones no figurales. Estos niveles son:
1. Pequeños alineamientos.
2. Alineamientos continuos (con cambio de criterio) u objetos colectivos.
3. Pequeñas colecciones yuxtapuestas sin criterio único y con un residuo heterogéneo.
4. Colecciones sin criterio único pero sin residuo ni intersecciones.
5. Colecciones con un criterio único, sin residuo ni intersecciones.
6. Colecciones con subdivisiones.
7. Clases.
Por tanto, el rango de la puntuación era 1-7, según se adscribieran a uno u otro de estos niveles genéticos.
Sólo se utilizaron criterios de clasificación aditiva porque los esquemas numéricos a los que hace referencia el presente trabajo de investigación tienen un carácter lineal (unidimensional) y, en este sentido, aditivo.
La segunda parte de la prueba se ajusta a los mismos patrones que la anterior, la única diferencia estriba en que el material puede ser organizado, tanto desde la perspectiva de clases lógicas (teoría lógica de Piaget), como desde la de clases colectivas (teoría mereológica de Lesniewski). En efecto, la clase de los soldados puede ser sustituida por el ejército y sus posibles subdivisiones soldados a caballo y soldados a pie pueden ser sustituidas, respectivamente, por caballería e infantería, eliminando así las posibles deficiencias que pueda presentar la tarea con un material de formas geométricas (Carbonnel, 1978; Gerstl y Pribbenow, 1995; Lesniewski, 1989; Markman, 1978; 1979; Markman, Horton y McLanahan, 1980; Markman y Seibert, 1976; Mieville, 1984; Serrano y Fernández, 1989).
Prueba de seriación
Esta prueba, aunque retiene algo de los trabajos piagetianos (ítem 6), está basada fundamentalmente en las investigaciones de J. Kingma y J. Reuvekamp (1984) y consta de seis ítems. La consigna para los cinco primeros ítems era: “Mira estos monigotes, están en desorden. Tu tienes que encontrar la manera de arreglarlos”.
Ítem 1: Seriación por longitud
Material: El material está compuesto por nueve rectángulos de dos dimensiones que representan monigotes con corbatas de pajarita. La anchura de estos rectángulos es irrelevante por cuanto, al tener dos de ellos la misma anchura, no es posible la seriación a partir de esta dimensión y, por tanto, ésta debe hacerse en función de su longitud.
Ítem 2: Seriación por la anchura
Material: Siete rectángulos de dos dimensiones que representan monigotes con corbatas de pajarita. La longitud de estos rectángulos es irrelevante y la seriación debe hacerse en función de su anchura ya que dos de ellos tienen la misma longitud y, por tanto, no existe posibilidad de seriación en función de esta dimensión.
Ítem 3: Seriación por la altura
Material: El material consta también de siete rectángulos, similares a los anteriores, que representan monigotes con corbatas de pajarita. Tanto la longitud como la anchura de estos rectángulos es irrelevante y la seriación debe hacerse (no se considera el grosor que, por otra parte, es el mismo para todos los rectángulos) en función de la altura a la que se encuentran las corbatas de pajarita. Esto se debe a que dos de ellos presentan la misma longitud y otros dos la misma anchura, lo que impide la posibilidad de establecer la seriación en función de estas dos dimensiones.
Ítem 4: Seriación por la longitud
Material: El material consta de siete paralelepípedos que representan monigotes con corbatas de pajaritas. La anchura, el grosor y el peso de estos rectángulos es irrelevante y la seriación debe hacerse en función de la longitud (altura de los monigotes) de los mismos, puesto que dos de ellos tienen la misma anchura, dos tienen el mismo grosor y otros dos tienen el mismo peso y, por tanto, no es posible la seriación en función de ninguna de estas tres dimensiones.
Ítem 5: Seriación por el peso
Material: El material consta de cinco paralelepípedos que representan monigotes con corbatas de pajarita. La anchura, el grosor y la altura de estos rectángulos es irrelevante y la seriación debe hacerse en función del peso de los mismos, ya que dos de ellos tienen la misma anchura, dos presentan el mismo grosor y, finalmente, existen otros dos con la misma altura y, por tanto, no es posible la seriación en función de ninguna de estas tres dimensiones.
Ítem 6: Seriación por la longitud
Material: Siete cilindros de longitudes diferentes (con una diferencia de 2 cms.) y una plataforma con agujeros para insertar los cilindros. La separación entre los agujeros es de 6,5 cms. La consigna para este ítem era: “Mira estos palos. Debes encontrar la manera de colocarlos (ordenarlos) de la mejor forma posible introduciéndolos en los agujeros”.
En esta prueba cada ítem acertado se valoraba con un punto. El rango de puntuación que presenta la prueba de seriación es, por tanto, de 0 a 6.
Es necesario hacer constar que, en todas las situaciones, el experimentador explicaba a los pequeños las características de los elementos a ordenar.
Pruebas numéricas
Para medir la variable número optamos por establecer tres tipos de pruebas. En efecto, Piaget cuando habla de “conservación del número”, lo hace identificándolo con “conservación de la cantidad numérica”, es decir, para Piaget el número siempre es la expresión de la medida de una cantidad, por tanto, tenemos que admitir la existencia de dos niveles de medida que hacen referencia a las clásicas pruebas de conservación piagetiana sobre las cantidades discretas y continuas (Piaget y Szeminska, 1975). Sin embargo, uno de nosotros había elaborado una prueba, ad hoc, de composición y descomposición numérica (sobre situaciones numéricas y empíricas), que se mostró ampliamente consistente en el modelo de medida que utilizó en su experiencia sobre aplicación de un sistema de ecuaciones estructurales para determinar los esquemas cognitivos implicados en la adquisición del número (Serrano, 2005).
La primera de las medidas, que hemos denominado conservación de las cantidades discretas, esta basada en la tarea piagetiana del mismo nombre (Piaget y Szeminska, 1975; pp. 43-56) pero con ciertas modificaciones introducidas por Gréco (1960; 1962) y por Serrano (1982).
Material: El material utilizado en esta prueba esta formado por un juego comercial de damas, es decir, que consta de doce fichas blancas y doce negras de tamaño habitual en un juego de este tipo: tres o cuatro centímetro de diámetro.
Técnica y consignas: El experimentador le dice al niño (mostrándole los dos conjunto de fichas del juego): “Vamos a jugar con estas fichas a un juego que yo he inventado, ¿Con cuáles quieres jugar tú, con las blancas o con las negras?”. Una vez que el niño ha escogido uno de los dos conjuntos de fichas (supongamos que escoge las negras) el experimentador le dice: “Bien, yo jugaré con la otras (en nuestro caso, las blancas)”.
Una vez definido el color de las colecciones del experimentador y del niño, se comienza la prueba. Hemos de tener en cuenta que los ítems o secuencias de esta tarea cognitiva presentan una dependencia lineal y, como ya se demostró cuando fueron jerarquizados mediante un estudio de validación convergente (Serrano, 1982), el fracaso en uno cualquiera de estos ítems excluye la posibilidad de acierto en todos los que le suceden.
El experimentador comienza la tarea colocando siete fichas de su conjunto (blancas) en línea recta y con la separación aproximada del diámetro de una de las fichas, es decir, tres o cuatro centímetros. A continuación le dice al niño: “Mira las fichas que yo he puesto y después pon tú, aquí abajo, las mismas fichas que yo (o el mismo número de fichas que yo)”.
Si el sujeto no es capaz de establecer la identidad (aunque sea de forma pseudocuantitativa) se interrumpe la prueba y se le concederá cero o un punto, en función del nivel genético (los distintos niveles genéticos son descritos al final de las tareas de conservación) al que sea asignada su conducta.
Si, por el contrario el sujeto es capaz de establecer una identidad de tipo cuantitativo o pseudocuantitativo (fundamentalmente, como se puede constatar de forma empírica, a partir de los esquemas de correspondencia biunívoca), se le interrogará acerca de la construcción de un conjunto más o menos numeroso que el dado por el experimentador, diciéndole: “Bien, retira tus fichas”. Una vez hecho, el experimentador continúa: “Ahora tienes que poner más fichas que yo”. Tanto si realiza o no correctamente la construcción de un conjunto más numeroso que el dado, se le pide la de un conjunto menos numeroso: “Bien, retira tus fichas”. Una vez hecho se le dice: “Ahora tienes que poner menos fichas que yo”.
Si el niño no es capaz de construir un conjunto más numeroso y menos numeroso que el dado por el experimentador (con siete fichas) se suspende la prueba y se le asigna al nivel genético correspondiente que marcará su puntuación en la prueba.
Si fuera capaz de construir un conjunto menos numeroso que el dado, pero fracasara en la construcción de un conjunto más numeroso, el experimentador, para realizar una subprueba de confirmación, procedía de la manera que detallamos a continuación. En primer lugar, retiraba su colección de fichas y volvía a colocar una nueva que tenía los mismos elementos que la colección construida por el niño y que le había llevado al éxito en la construcción de un conjunto menos numeroso que el inicialmente dado por el experimentador, que como se recordará tenía siete elementos, al mismo tiempo que se le decía: “Mira, yo también quito mis fichas y ahora pongo éstas. Por tú más fichas que yo”. Si, tras la nueva situación, en la construcción de un conjunto más numeroso se vuelve a fracasar, se puede pensar, con una alta probabilidad de acierto, que el éxito de la situación anterior pudo ser debido al azar y, por tanto, situaremos al sujeto en el nivel genético que corresponde al fracaso de las dos situaciones (construcción de un conjunto más numeroso y un conjunto menos numeroso). Si, por el contrario, ante la nueva situación se invirtieran los términos y encontráramos una conducta de acierto para la construcción de un conjunto más numeroso y una conducta de fracaso para la construcción de un conjunto menos numeroso, se podría concluir que el éxito o el fracaso de la prueba está condicionado al número de elementos de la misma y, tras suspender la prueba, asignaríamos al sujeto la puntuación 3 correspondiente al nivel genético de “asociación de los vectores (objetivos) a los escalares (subjetivos)”.
Si la construcción de un conjunto con más o menos elementos que la colección testigo hubiera sido exitosa, la prueba continuaría de la siguiente manera:
En primer lugar se le pedía al niño que restableciera de nuevo la igualdad: “Pon, de nuevo, las misma fichas que yo” y, una vez lograda, se desplazaban las fichas de la colección testigo, de tal manera que la penúltima ficha quedara en “correspondencia óptica” con la última ficha de la colección formada por el niño, al tiempo que se decía: “¡Mira!, ahora yo voy a mover mis fichas, como ves no quito ni pongo ninguna, solamente las muevo”. Una vez completada la operación de desplazamiento se le volvía a interrogar sobre la igualdad que acababa de construir, diciendo: “Y ahora, tenemos las mismas?”.
1. Si la respuesta era negativa, se le preguntaba, en primer lugar, por la numerosidad de ambas colecciones: “¿Cuántas fichas tengo yo?, ¿Y tú?”, para, a continuación, interrogarles sobre la acción que debía realizar con el fin de mantener la igualdad inicial: “¿Y qué debemos hacer para tener las mismas?”. Dos posibles soluciones (a y b) daban los sujetos a las demandas del experimentador:
a. Para la primera pregunta, y tras repetir que ambas colecciones tenían siete elementos, mantenían la desigualdad (7 ¹ 7): “Tú tienes siete y yo tengo siete, pero tú tienes más que yo”. Para la segunda pregunta, la solución apuntaba a añadir una ficha más a su colección, con el fin de establecer la igualdad perceptiva. Si se les interrogaba en esta nueva situación sobre la igualdad numérica llegaban a la conclusión de que 7 = 8: “Ahora tú tienes siete y yo tengo ocho”, el experimentador preguntaba: pero, ¿tenemos las mismas?. La respuesta por parte de los sujetos de este nivel (confusión de los esquemas de adición y desplazamiento) es siempre afirmativa.
b. En este nivel más evolucionado (diferenciación de los esquemas de adición y desplazamiento, pero sin integración en una estructura total de conjunto), los sujetos experimentaban ciertas turbaciones ante la contradicción 7 ¹ 7. Con relación a la segunda cuestión, la solución apuntaba a un desplazamiento en sentido inverso, no admitiendo nunca la solución de adición (reversibilidad empírica o retorno empírico). Para confirmar esta diferenciación de esquemas, el experimentador realizaba la contraprueba siguiente: partiendo de la posición inicial de correspondencia uno-a-uno, se añadía una ficha a la colección testigo, y se planteaban de nuevo todas las cuestiones. La solución para esta situación era la de compensar la perturbación con otra adición en su colección o eliminar (restar) la ficha añadida a la colección del experimentador.
2. Si la respuesta era afirmativa y el pequeño mantenía la igualdad, pese al desplazamiento, se le pedía que diera el argumento de reversibilidad operatoria (¿por qué?) que había utilizado y se realizaban algunas contra-argumentaciones (“pero mi fila es más larga que la tuya”, etc.) para confirmar el nivel.
Esta prueba presenta, en función de los niveles genéticos, un rango de cero a seis.
La segunda medida del constructo de número, que hemos denominado conservación de las cantidades continuas, está basada, igualmente, en la tarea piagetiana del mismo nombre (Piaget y Szeminska, 1975; pp. 43-56) pero también con ciertas modificaciones (Serrano, 1982). Hemos de tener en cuenta que, por ser una tarea piagetiana, es isomorfa a la anterior y los ítems, secuencias o niveles genéticos son idénticos en ambas tareas.
Material: El material utilizado en esta prueba está formado por un vaso grande; dos juegos idénticos formados, cada uno, por otro vaso grande (distinto del anterior en cuanto a forma, pero de la misma capacidad) y cinco vasos pequeños, idénticos entre sí y cuya suma de capacidades es equivalente a la de uno de los vasos grandes; dos tipos de refrescos (de naranja y de limón) y dos muñecas cuyo color de pelo y de vestido es similar al de los refrescos, a fin de reforzar las relaciones de correspondencia y de pertenencia.
Técnica y consignas: El experimentador le dice al niño, al mismo tiempo que le muestra los dos vasos grandes idénticos, las muñecas y las botellas de refrescos: “Vamos a jugar con estas cosas a un juego que yo he inventado y que se llama fiesta de cumpleaños. En este juego hay dos amiguitas nuestras que son las dos que ves aquí (le muestra las dos muñecas). Una (la de color anaranjado) quiere refresco de naranja y la otra (la de color amarillo) quiere refresco de limón. Yo voy a ponerle a ésta su refresco de naranja (el experimentador vierte el refresco de naranja de la botella en el vaso, hasta un nivel próximo al setenta y cinco por ciento de la altura total del vaso)”. Una vez ejecutada la acción se le dice al pequeño: “Ves, ¡ya está!. Ahora debes servir tú el refresco de limón a la otra muñeca, pero ¡cuidado!, debes ponerle lo mismo de limón (o, la misma cantidad, o, igual) que yo le puse a ésta (se le pueden dar nombres a las muñecas para simplificar la nomenclatura) de naranja”.
Si el sujeto no es capaz de establecer la identidad se interrumpe la prueba y se le concederá cero o un punto, en función del nivel genético (los distintos niveles genéticos son descritos, como ya se ha dicho, al final de las tareas de conservación) al que sea asignada su conducta.
Si, por el contrario el sujeto es capaz de establecer una identidad de tipo cuantitativo o pseudocuantitativo, se le interrogará acerca de la construcción de una entidad con mayor o menor cantidad que la dada por el experimentador, diciéndole tras vaciar el vaso de refresco de limón: “Ahora tienes que ponerle a la muñeca más (cantidad) refresco de limón que el que yo le he puesto de naranja a la otra, sin que ésta se dé cuenta (se vuelve la primera muñeca simulando un pequeño descuido)”. Lo mismo se hace a continuación, pidiéndole que ponga menos.
Si el niño no es capaz de construir situaciones de desigualdad (mayor y menor cantidad que) se suspende la prueba y se le asigna al nivel genético correspondiente que marcará su puntuación en la prueba.
Si fuera capaz de solucionar el problema cuando se le pide que ponga menos cantidad que una dada, pero fracasará en la construcción de una entidad mayor que otra, el experimentador, para realizar una subprueba de confirmación (al igual que se hacía con las cantidades discretas), procedía de la manera que detallamos a continuación. En primer lugar, retiraba el líquido del vaso que estaba sirviendo como testigo y volvía a colocar una nueva cantidad que alcanzaba la misma altura que la entidad construida por el niño y que le había llevado al éxito en la solución del problema planteado con el uso del “menos que...” dado, inicialmente por el experimentador, al mismo tiempo que se le decía: “Mira, yo le quito el refresco de naranja y ahora pongo naranja por aquí. Pon tú, ahora, más refresco de limón que el que yo he puesto de naranja”. Si, tras la nueva situación, en la construcción de una cantidad mayor se vuelve a fracasar, se puede pensar, con una alta probabilidad de acierto, que el éxito del problema anterior pudo ser debido al azar y, por tanto, debemos situar al sujeto en el nivel genético que corresponde al fracaso de la dos situaciones (construcción del más y del menos en problemas que impliquen la manipulación en cantidades continuas. Si, por el contrario, ante la nueva situación se invirtieran los términos y encontráramos una conducta de acierto para la construcción de una cantidad mayor y una conducta de fracaso para la construcción de una cantidad menor, se podría concluir que el éxito o el fracaso de la prueba está condicionado al tamaño de las cantidades utilizadas en la misma y, tras suspender la prueba, asignaríamos al sujeto la puntuación “tres” correspondiente al nivel genético de “asociación e los vectores (objetivos) a los escalares (subjetivos)”.
Si la construcción de una entidad con más o menos cantidad que otra dada hubiera sido exitosa, la prueba continuaba de la siguiente manera:
En primer lugar se le pedía al niño que restableciera de nuevo la igualdad a través de la construcción de una unidad, diciéndole: “¡Mira! ahora, para que no se beban todo el refresco de golpe y no les haga daño, se lo vamos a poner en estos vasos pequeños. ¡Ves!, yo le pongo a una muñeca en estos vasos pequeños lo mismo que tenía en el vaso grande (un vaso grande llena cinco pequeños). Pon tú a esta muñeca la misma cantidad de refresco de limón que yo le he puesto a ésta de naranja”. Una vez conseguido el establecimiento de la igualdad, se interrogaba al niño sobre el número de unidades (vasos pequeños) que cabían en un vaso grande y se hacían experiencias de trasvase y de adición y sustracción de unidades como, por ejemplo: “Ahora que está la muñeca descuidada bébete un vaso pequeño de refresco”. Tras hacerlo, se volvía a la situación primitiva (sobre los vasos grandes) pero, evidentemente, ahora una muñeca tenía en su vaso cuatro unidades y la otra cinco (lo que supone menos cantidad y menos altura). En esta nueva situación se le interrogaba de nuevo sobre la igualdad-desigualdad, pidiendo el argumento de desigualdad. Familiarizado el sujeto con la posibilidad del manejo de la unidad iterable (y por tanto del número) se reconstruía la igualdad de las cantidades de refresco (a partir de las cinco unidades) y, una vez aceptada, se le decía: “¡Mira!, ahora yo voy a poner el refresco de naranja en este otro vaso (más largo y estrecho), como ves no quito ni pongo ningún vasito, solamente pongo el refresco de naranja en este vaso nuevo”. Completada la operación de desplazamiento se le volvía a interrogar sobre la igualdad que acababa de construir, diciendo: “Ahora, ¿tienen las dos muñecas la misma cantidad de refresco? o ¿pueden beber las dos lo mismo de refresco?” (las consignas estaban adaptadas a la capacidad semántica del sujeto).
1. Si la respuesta era negativa, se le preguntaba, en primer lugar, por la numerosidad de ambas cantidades: ”¿Cuántos vasitos tiene esta puede esta beber?, ¿y aquélla?”, para, a continuación interrogarles sobre la acción que debía realizar con el fin de mantener la igualdad inicial: “¿Y qué debemos hacer para tener la misma cantidad?”. Las posibles soluciones que daban los sujetos a las demandas del experimentador eran las siguientes:
a. Para la primera pregunta, y tras repetir que ambas cantidades tenían cinco elementos (unidades o vasitos) mantenían la desigualdad (5 ¹ 5):”Esta tiene cinco y aquélla también, pero esta tiene más que aquélla”. Para la segunda pregunta, la solución apuntaba a añadir mas refresco al vaso donde el refresco alcanzaba menor altura con el fin de establecer la igualdad perceptiva.
b. En este nivel, más evolucionado (diferenciación de los esquemas de adicción y desplazamiento, pero sin integración en una estructura total de conjunto), los sujetos experimentaban ciertas turbaciones ante la contradicción 5 ¹ 5. Con relación a la segunda cuestión, la solución apuntaba a un desplazamiento en sentido inverso, no admitiendo nunca la solución de adicción (reversibilidad empírica o retorno empírico). Para confirmar esta diferenciación de esquemas el experimentador realizaba la contraprueba siguiente: partiendo de la posición inicial sobre los dos vasos idénticos se añadía una unidad al refresco de una de las muñecas, y se planteaban de nuevo todas las cuestiones. La solución para esta situación era la de compensar la perturbación con otra adición en el otro refresco o eliminar (restar) la unidad añadida al primer refresco por parte del experimentador.
c. Si la respuesta era afirmativa y mantenía la igualdad, pese al trasvase del refresco, se le pedía que diera el argumento de reversibilidad (¿por qué?) y se realizaban algunas contra argumentaciones (“pero este vaso es más alto”, etc.) para confirmar el nivel.
Hemos de destacar que las condiciones del material favorecían la generación de determinadas contradicciones, con la consiguiente posibilidad de superaciones, que podían ser conducentes a una noción de conservación. En efecto, en los vasos grandes las dimensiones del vaso largo y estrecho, en relación con las dimensiones de cualquiera de los dos vaso, cortos y anchos, presentaban las siguientes características: cuando ambos albergaban cinco unidades, la altura alcanzada por el refresco era, de forma bastante perceptible, mayor en el vaso estrecho que en el ancho, pero cuando ambos diferían en una unidad (seis unidades en el vaso ancho y cinco en el estrecho o cinco unidades en el ancho y cuatro en el estrecho) la altura seguía siendo ligeramente mayor en el vaso estrecho, es decir, en el vaso que menos unidades de refresco contenía. Esto suponía una manifiesta contradicción entre los aspectos perceptivos y numéricos de la tarea.
Esta prueba presenta, en función de los niveles genéticos, un rango de puntuación idéntico al de la prueba anterior, es decir, de cero a seis.
Serrano (1980; 1982) ha podido constatar, en este tipo de tareas, hasta seis conductas distintas que se podrían distribuir en dos grandes grupos: uno sobre la construcción de la identidad cualitativa (que abarca los niveles 1, 2 y 3) y otro sobre la consecución de la identidad cuantitativa (que abarca los niveles 4, 5 y 6), además de un nivel previo (nivel 0) que “es el punto de partida de toda adquisición referida al número o a cualquier otro concepto” (Serrano, 1982; pp. 353-354).
Finalmente, y como dijimos con anterioridad, una prueba de composición y descomposición del número fue aplicada como tercera medida para el constructo de número.
Esta prueba constaba de doce ítems y estaba dividida en dos subpruebas. La puntuación de cada ítem era 0 ó 1, teniendo en cuenta que los dos últimos ítems de cada subprueba (ítems 6 y 12), al tener que dar una solución doble, si sólo daba una de ellas se puntuaba con 0’5. La primera, que podríamos denominar “composición y descomposición del número en situaciones empíricas” consta de seis ítems.
Material: El material utilizado en esta prueba estaba formado por dos muñecas, como las descritas para las pruebas de conservación para las cantidades continuas, es decir, una con el pelo y el vestido naranja y otra con el pelo y el vestido amarillo, caramelos naranjas y amarillos, una caja y tarjetas cuadradas con los números: 1, 2, 3, 4, 5, 6, 7, 8, y 9.
Ítem 1: Composición empírica de un conjunto a partir de dos subcolecciones dadas, con elementos diferenciados
Material: Dos muñecas, dos caramelos naranjas, un caramelo amarillo y una caja.
Técnica y consignas: Se le presentan al niño las dos muñecas, una al lado de la otra, con una separación aproximada de 20 cms. Junto a ellas y a una separación de la segunda muñeca de alrededor de 30 cms., se coloca la caja. Bajo la muñeca (naranja) se colocan dos caramelos del mismo color (naranja) y debajo de la amarilla, un caramelo de color amarillo, al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la naranja) tiene dos caramelos y ésta (la amarilla) tiene un caramelo (se le da en este momento el conjunto de todos los caramelos naranjas y amarillos salvo, evidentemente, los que se le han dado a las muñecas). Ahora tienes que poner dentro de esta caja los mismos caramelos que tienen las dos muñecas juntas”.
Ítem 2: Composición empírica de un conjunto a partir de dos subcolecciones dadas, con elementos no diferenciados
Material: Dos muñecas, nueve caramelos naranja y una caja.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Junto a ellas y a una separación de la segunda muñeca de alrededor de 30 cms., se coloca la caja. Bajo la muñeca (naranja) se colocan seis caramelos del mismo color (naranja) y debajo de la amarilla, tres caramelos de color, igualmente rojos, al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la naranja) tiene seis caramelos y ésta (la amarilla) tiene tres (se le da en este momento el conjunto de todos los caramelos naranjas y amarillos salvo, evidentemente, los que ya se le han dado a los muñecas). Ahora tienes que poner dentro de esta caja los mismos caramelos que tienen las dos muñecas juntas”.
Ítem 3: Descomposición empírica de un conjunto, dados los elementos del conjunto y de una de las subcolecciones, con elementos diferenciados
Material: Dos muñecas, seis caramelos naranja, dos caramelos amarillos y una caja.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Junto a ellas y a una separación con respecto de la segunda muñeca de alrededor de 30 cms., se coloca la caja. Debajo de la muñeca (naranja) se colocan tres caramelos del mismo color (naranja) y dentro de la caja, tres caramelos de color naranja y dos de color amarillo, al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la de color naranja) tiene tres caramelos y dentro de la caja hemos puesto los caramelos que tienen entre las dos muñecas juntas (en este momento, se le da el conjunto de todos los caramelos naranjas y amarillos, salvo, evidentemente, los que se han puesto dentro de la caja y los que se le dieron a la muñeca naranja). Ahora tienes que darle tú a la muñeca amarilla los caramelos que le correspondan y para ello no debes olvidar que dentro de la caja están los caramelos que tienen las dos muñecas juntas”.
Ítem 4: Descomposición empírica de un conjunto, dados los elementos del conjunto y de una de las subcolecciones, con elementos no diferenciados
Material: dos muñecas, doce caramelos todos de color naranja, y una caja.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Junto a ellas y a una separación con respecto de la segunda muñeca de alrededor de 30 cms., se coloca la caja. Debajo de la muñeca (naranja) se colocan cinco caramelos del mismo color (naranja) y dentro de la caja, doce caramelos, también de color naranja, al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la de color naranja) tiene cinco caramelos y dentro de la caja hemos puesto los caramelos que tienen entre las dos muñecas juntas (en este momento, se le da el conjunto de todos los caramelos naranjas y amarillos, salvo, evidentemente, los que se han puesto dentro de la caja y los que se le dieron a la muñeca de color naranja). Ahora tienes que darle tú a la muñeca de color amarillo los caramelos que le correspondan y para ello no debes olvidar que dentro de la caja están los caramelos que tienen las dos muñecas juntas”.
Ítem 5: Descomposición empírica de un conjunto en forma aleatoria
Material: dos muñecas, seis caramelos naranjas, y una caja.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Junto a ellas y a una separación de la segunda muñeca de alrededor de 30 cms., se coloca la caja. Dentro de la caja se colocan los seis caramelos y se le dice: “¡Mira!, en esta caja están los caramelos de las dos muñecas (se le da en este momento el conjunto de todos los caramelos naranjas y amarillos, salvo, evidentemente, los que se han puesto dentro de la caja). Ahora tienes que poner debajo de las muñecas los caramelos que tú creas que le corresponden a cada una y para ello no debes olvidar que dentro de la caja hemos puesto los caramelos que tienen las dos muñecas juntas”.
Ítem 6: Conmutabilidad y asociatividad en la situación anterior
Material: El mismo que para la situación anterior.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior y se le dice: “¡Mira!, como ya hemos visto antes, en esta caja están los caramelos de las dos muñecas (se le da en este momento el conjunto de todos los caramelos naranjas y amarillos salvo evidentemente, los que se han colocado en la caja). Ahora tienes que poner debajo de las muñecas los caramelos que tú creas que le corresponden a cada una, pero tienes que hacerlo de diferente manera a como lo hiciste con anterioridad. No debes olvidar que dentro de la caja hemos puesto los caramelos que tienen las dos muñecas juntas. Vamos a ver de cuántas formas eres capaz de hacerlo”.
La segunda de las subpruebas (“composición y descomposición del número en situaciones numéricas”) consta, igualmente, de seis ítems isomorfos con los anteriores.
Ítem 7: Composición aritmética de un conjunto a partir de dos subcolecciones dadas
Material: Dos muñecas, cinco caramelos naranjas y un conjunto de cartulinas que llevan dibujadas los nueve primeros números.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Bajo la muñeca (naranja) se colocan cuatro caramelos naranja y debajo de la amarilla, un caramelo también naranja, al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la naranja) tiene dos caramelos y esta (la amarilla) tiene un caramelo (se le da en este momento el conjunto de todas las tarjetas con números). Ahora tienes que escoger de entre estas tarjetas la que tiene el número que indica cuántos caramelos tienen las dos muñecas juntas”.
Ítem 8: Composición aritmética de dos números
Material: Dos muñecas y un juego de tarjetas que contienen los nueve primeros números.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Bajo la muñeca (naranja) se coloca una tarjeta con el número 3 y debajo de la amarilla, otra tarjeta con el número 4, al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la naranja) tiene una tarjeta que nos dice cuántos caramelos tiene y esta (la amarilla) tiene también una tarjeta que indica el número de caramelos que tiene guardado (se le da en este momento el conjunto de todas las tarjetas con números). Ahora tienes que escoger de entre estas tarjetas aquélla que tiene el número que indica cuantos caramelos tienen las dos muñecas juntas”.
Ítem 9: Descomposición empírica de un número en dos subcolecciones, con elementos diferenciados o no diferenciados, conocida una de ellas
Material: Dos muñecas, un conjunto de caramelos naranjas y amarillos y una tarjeta con el número 3.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Debajo de la muñeca (naranja) se coloca un caramelo naranja y, junto a los muñecas una tarjeta con el número 3 al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la naranja) tiene un caramelo y esta tarjeta indica el numero de caramelos que tienen las dos muñecas juntas (se le da en este momento el conjunto de todos los caramelos). Ahora tienes que poner debajo de la muñeca amarilla el número de caramelos que tiene ella sola. No olvides que la tarjeta te dice cuantos caramelos tienen entre las dos muñecas”.
Ítem 10: Descomposición aritmética de un número en dos, conocido uno de ellos
Material: Dos muñecas y cartulinas con los nueve dígitos.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Debajo de la muñeca naranja se coloca una cartulina con el número 7 y junto a las muñecas, y sobre ellas, una tarjeta con el número 9 al mismo tiempo que se le dice: “¡Mira!, esta muñeca (la naranja) tiene debajo un número que nos dice cuántos caramelos tiene guardados y esta tarjeta indica el número de caramelos que tienen las dos muñecas juntas (se le da en este momento el conjunto de todas las tarjetas). Ahora tienes que poner debajo de la muñeca amarilla una tarjeta que nos indique el número de caramelos que tiene ella sola. No olvides que la tarjeta te dice cuántos caramelos tienen entre las dos muñecas”.
Ítem 11: Descomposición numérica aleatoria
Material: Dos muñecas y un juego de cartulinas con los nueve dígitos.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en ítem anterior. Junto a ellas, y a una separación de la segunda muñeca de 30 cms., se coloca una tarjeta con el número 6 al mismo tiempo que se le dice: “¡Mira!, esta tarjeta nos dice el número de caramelos que tienen las dos muñecas (se le da en este momento el conjunto de todas las tarjetas salvo, evidentemente, la que se ha colocado junto a las muñecas). Ahora tienes que poner debajo de las muñecas las tarjetas con los números que tú creas que le corresponden a cada una y para ello no debes olvidar que esta tarjeta nos dice el número de caramelos que tienen las dos muñecas juntas”.
Ítem 12: Conmutatividad y asociatividad en la situación anterior
Material: El mismo que para la situación anterior.
Técnica y consignas: Se presenta el material de la misma forma que se presentó en el ítem anterior y se le dice: “¡Mira!, como ya hemos visto antes, esta tarjeta nos dice el número de caramelos de las dos muñecas (se le da en este momento el conjunto de todas las tarjetas salvo, evidentemente, la que se ha colocado junto a las muñecas). Ahora tienes que poner debajo de las muñecas las tarjetas con los números que tú creas que le corresponden a cada una, pero tienes que hacerlo de diferente manera a como lo hiciste con anterioridad. No debes olvidar que esta tarjeta no dice el número de caramelos que tienen las dos muñecas juntas. Vamos a ver de cuántas formas eres capaz de hacerlo”.
3. Análisis de datos. Los datos de esta matriz fueron analizados mediante tres análisis de varianza factorial con el paquete estadístico SYSTAT versión 10.0 (2000).
El primero de los análisis de varianza considera, como variable dependiente la conservación de las cantidades discretas, como variables independientes (covariables) la clasificación y la seriación, actuando el nivel como factor de clasificación. Los resultados de este análisis se reflejan en la tabla 1.
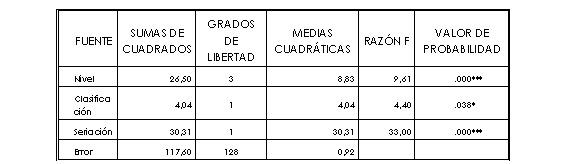
El modelo explica el 65’7% de la variable dependiente (r2 = 0,657).
La covariante seriación resulta altamente significativa (1‰) y aunque la variable clasificación también resulta significativa, su nivel de significación es sensiblemente menor (5%). Por último, las diferencias de niveles manifiestan un comportamiento significativamente diferente (1‰).
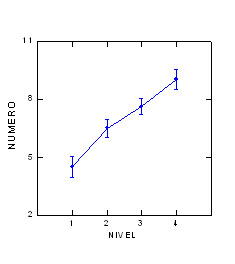
Como se puede observar directamente en el gráfico I las diferencias internivel se dan entre los niveles 1 contra 2; 1 contra 3; 1 contra 4; 2 contra 4 y 3 contra 4, no apareciendo diferencias en la comparación entre los niveles 2 y 3.
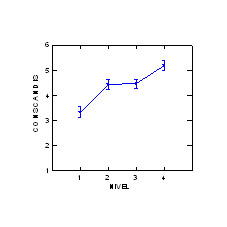
El análisis de varianza efectuado en segundo lugar considera, como variable dependiente la conservación de las cantidades continuas, como variables independientes (covariables) la clasificación y la seriación, actuando el nivel como factor de clasificación. Los resultados de este análisis se reflejan en la tabla 2.
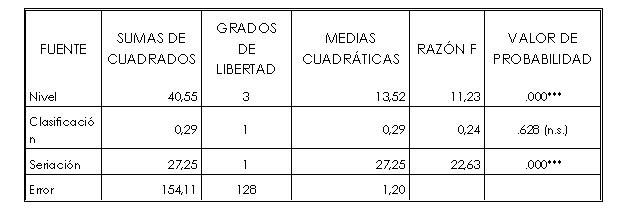
El modelo explica el 55’7% de la variable dependiente (r2 = 0,557).
La covariante seriación resulta altamente significativa (1‰). Sin embargo, en este modelo, la variable clasificación no resulta significativa.
Con relación al factor de agrupamiento, se puede comprobar que los sujetos adscritos a los distintos niveles muestran un comportamiento diferente ante la variable dependiente del modelo y estas diferencias presentan un alto nivel de significación (1‰).
Estas diferencias internivel se comportan igual que en el caso anterior (Gráfico II).
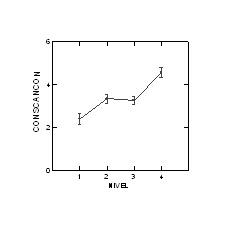
Finalmente, el tercero de los análisis de varianza considera, como variable dependiente la prueba específica de número y como variables independientes (covariables) la clasificación y la seriación, actuando el nivel como factor de clasificación.
Los resultados de este análisis se reflejan en la tabla 3.
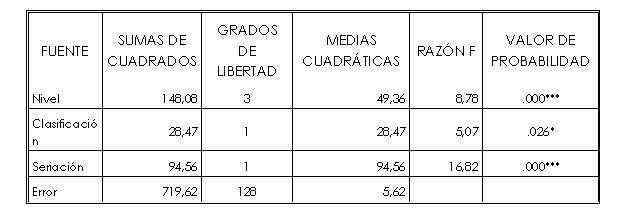
El modelo explica el 61’9% de la variable dependiente (r2 = 0,619).
La covariante seriación resulta altamente significativa (1‰) y aunque la variable clasificación también resulta significativa, su nivel de significación es sensiblemente menor (5%, a £. 026). Por último, las diferencias de niveles vuelven a manifestar un comportamiento significativamente diferente (1‰).
Sin embargo, ahora, como se puede observar en el gráfico 3 estas diferencias entre niveles se dan entre todas las comparaciones posibles.
CONCLUSIONES Y DISCUSIÓN: IMPLICACIONES INSTRUCCIONALES.
A pesar de haber transcurrido mas de media centuria desde la publicación de La génesis del número en el niño y de La Génesis de las estructuras lógicas elementales, los trabajos iniciales de la Escuela de Ginebra siguen estando de actualidad, y las referencias a los mismos demuestran su vigencia, al menos, como punto de partida en cualquier proceso de enseñanza y aprendizaje en Educación Infantil, cuando los contenidos hacen referencia a la construcción del conocimiento lógico-matemático. No es pues de extrañar que la investigación siga ahondando en los trabajos piagetianos sobre la formación de los conocimientos (Scholnick, Nelson, Gelman y Miller (1999), especialmente en el campo de las matemáticas (English, 2002), y que el paradigma constructivista, que anega nuestras aulas, los tome como uno de sus elementos referenciales más destacados (Lesh y Doerr, 2003).
Nuestro trabajo trata de aportar algo más de luz en este campo, de manera que los profesionales de la educación, que se co-responsabilizan en la construcción de los pilares básicos del edificio lógico-matemático por los alumnos más pequeños, dispongan de más perspectivas de interpretación acerca de la construcción del número natural. En este sentido, y a partir de los resultados obtenidos, se puede concluir que existe un paralelismo en la ejecución de los sujetos entre la conservación de las cantidades continuas y discretas con un ligero desfase entre ambas, resultando una tarea más compleja la conservación de las cantidades continuas, como puede desprenderse de una simple confrontación entre los gráficos I y II. Esta situación pone de manifiesto que los procedimientos utilizados por los sujetos para alcanzar la conservación son muy distintos en un caso y otro. En efecto, la disponibilidad de los esquemas cuantificadores ante las demandas de la tarea de conservación de las cantidades continuas es menor que en la conservación de las cantidades discretas, tanto por el número de esquemas que están disponibles (las cantidades no pueden ser contadas), como por las acomodaciones deformantes que pueden efectuar los esquemas que el sujeto aplica, como es el caso del esquema de correspondencia uno-a-uno. Este esquema, se aplica en un momento del desarrollo de manera errónea y en lugar de establecer relaciones parte«parte el sujeto lo aplica para establecer relaciones todo«todo, comparando los niveles de líquido (cantidades continuas) o las longitudes (cantidades discretas). Sin embargo, esta conducta se mantiene durante mucho más tiempo en la primera situación que en la segunda ya que, las propias características de la tarea de conservación de las cantidades continuas, dificulta la puesta en marcha de algunos esquemas de cuantificación, lo que da origen al desfase horizontal que presentan estas dos tareas. De esta manera, sólo la coordinación de “esquemas cardinales” y “esquemas ordinales” confieren un significado no deformante a la tarea de conservación de las cantidades continuas, con lo que el número que es a la vez clase y orden no se encuentra disponible para dar solución al problema. Además, la resolución de la tarea de conservación de las cantidades continuas requiere una organización cognitiva bidimensional, es decir, organizar en un sistema de conjunto dos dimensiones (altura´anchura, por ejemplo). Esto supone una cierta contradicción en la obra de Piaget ya que si el número es una síntesis de los agrupamientos I y V (Piaget, 1977), la correcta resolución de la tarea de conservación de las cantidades continuas, al requerir una multiplicación biunívoca de clases y relaciones (agrupamientos IV y VIII) no puede ser una tarea de "número".
Desde una perspectiva psicopedagógica esta primera conclusión nos sugiere la primera de nuestras reflexiones. Por un lado, parece evidente que, en los primeros niveles, los sujetos evalúan las cantidades discretas como si fueran continuas, incluso aunque esté disponible el esquema de correspondencia uno-a-uno y, por otro, sabemos que para que un sujeto pueda conferir un significado no deformante a la realidad, la situación-problema planteada debe estar «próxima» a las capacidades cognitivas del sujeto a fin de que se posibilite un proceso de equilibración mayorante, es decir, hemos de partir de los que el sujeto sabe o cree saber y modificar estos saberes en la línea de los objetivos que pretendemos alcanzar. Entonces, si el sujeto cree que las cantidades son, de alguna manera, continuas, ¿por qué no partir de estas creencias y comenzar el proceso de enseñanza y aprendizaje por este tipo de cantidades para que el sujeto las discretice?, ¿no es el número un instrumento cognitivo para discretizar el continuo?.
La segunda de las conclusiones viene a poner en entredicho las teorías que postulan el origen psicológico del número desde una perspectiva reduccionista, bien por reducción a la lógica de clases, bien por reducción a las relaciones asimétricas y a las diferencias ordenadas, o a ambas a la vez, ya que el porcentaje de varianza explicado por las variables independientes deja, en el mejor de los casos (conservación de las cantidades discretas), casi un 35% de la varianza del constructo sin explicar. Esto conduce a pensar que el número presenta, al menos dentro de una perspectiva psicológica, unos componentes específicos y distintos a los de la lógica (sea una lógica de clases o de relaciones), bien porque las estrategias básicas de aprehensión sean distintas o bien porque la estructura numérica esté alimentada o constituida por unidades funcionales de conductas diferentes o distintos sistemas de relaciones. En el primero de los casos nos inclinamos por sugerir que la investigación debe continuar profundizando en las estrategias generales de selección y organización y en los procesos de atención ejecutiva (González, Fuentes, Carranza y Estévez, 2001). En el segundo caso, nos inclinamos a pensar que el sistema de relaciones que caracteriza la estructura numérica es diferente al que es propio de la estructura lógica y el propio Piaget (1977; pp. 236-243) reconoce que, en los agrupamientos de clases y relaciones, la asociatividad es incompleta, mientras que las conductas numéricas son asociativas y conforman una estructura de grupo. El paso de las operaciones intraproposicionales al número, es decir, de los agrupamientos lógicos a los grupos numéricos, debe configurar un nuevo sistema de relaciones y la transición entre un sistema y otro no queda suficientemente explicada por la teoría piagetiana.
En este sentido nadie discute que el número permite «cualificar» lo real, como nadie discute tampoco que permite establecer una «ordenación» en esa realidad cualificada, es decir, nadie discute que los esquemas numéricos tengan un componente o «principio cardinal» y un componente o «principio ordinal», como dirían Gelman y Gallistell (1978), pero la noción de «distinto» que establece Piaget (1977) no nos aporta a los educadores información suficiente para elaborar instrumentos de intervención en el aula que posibiliten la coordinación necesaria para que los esquemas cardinales y ordinales desemboquen en la construcción del número.
En tercer lugar, parece evidente que una simple mirada a las representaciones de los gráficos I y II, nos pone de manifiesto la ausencia de diferencias entre los sujetos de 5 y 6 años. Esta situación no se produce en la medida efectuada a partir de situaciones numéricas específicas (gráfico III). Todo ello nos sugiere que la propuesta de Piaget parece una solución macrogenética al problema y, por tanto, se debería continuar profundizando en la microgénesis inter-estadio para poder llegar a comprender el auténtico cambio comportamental del sujeto. En este sentido los trabajos actuales sobre la construcción del número en el niño apuntan en esa dirección (Smith, 1999; Sophian, 1995).
Estos resultados obligan a rechazar la hipótesis planteada en este trabajo ya que, si bien es cierto que el porcentaje de varianza explicado por el modelo es alto, resulta a todas luces insuficiente para plantear la construcción del número en términos de causa"efecto. Desde el punto de vista psicopedagógico, esto sugiere que las actividades de clasificación y seriación pueden ser un buen soporte para las actividades numéricas, pero actuando de forma complementaria a ellas, es decir, parafraseando un bonito trabajo piagetiano, clases, relaciones y números son contenidos instruccionales diferentes sobre los que actúan esquemas y sistemas relacionales distintos, con mecanismos asimiladores, probablemente diversificados y acomodaciones que confieren significados distintos a la realidad, aunque, sin lugar a dudas, se complementan entre sí para una mejor adaptación del sujeto a la realidad.
Utilizando términos piagetianos podríamos concluir que las estructuras lógicas elementales (clasificación y seriación) y las estructuras numéricas deben efectuar asimilaciones recíprocas a fin de llegar a construir el necesario sistema de cuantificación de lo real en el hombre. La práctica educativa debe tender, por tanto, a posibilitar estas asimilaciones recíprocas mediante actividades que conduzcan a establecer qué aportan las primeras a las segundas y viceversa, garantizando un desarrollo armónico entre ambas, con el fin de evitar cualquier tipo de desfase que genere un «desequilibrio» o una «laguna» en el sistema de cuantificación del sujeto.
Referencias bibliográficas
Becker, F. (1998): “Epistemologie génétique et pratique pédagogique”. Bulletin de Psychologie, 51; 613-622.
Brainerd, C.J. (1979): The origins of number concept. New York: Praeger.
Carbonnell, S. (1982): "Influence de la signification des objets dans les activités de classification". Enfance, 3; 193-210.
Ciancio, D.; Sadovsky, A.; Malabonga, V.; Truebllod, L. y Pasnak, R. (1999): “Teaching classification and seriation to preschoolers”. Child Study Journal, 29(3); 193-205.
Collette, J.P. (1985): Historia de las matemáticas. Vol. 1. Madrid: Siglo XXI.
English, L. (ed.) (2002): Handbook of International Research in Mathematics. Mahwah, NJ: Lawrence Erlbaum Associates.
Garret, K.N.; Busby, R.F. y Pasnak, R. (1999): “Cognitive gains from extended play at classification and seriation”. Journal of Research and Development in Education, 32(4); 257-263.
Gelman, R. y Gallistel, C. (1978): The Child’s Understanding of Number. Cambridge, MA: Harvard University Press.
Gerstl, P. y Pribbenow, S. (1995): “Midwinters, end games, and body parts: A classification of part-whole relations”. International Journal of Human Computer Studies, 43(5/6); 865-889.
Ghyka, M. (1978): Philosophie et mystique du nombre. Paris: Payot.
González, C.; Fuentes, L..; Carranza, J.A. y Estévez, A.F. (2001): “Temperament and attention in the self-regulation of 7-year-old children”. Personality and Individuals Differences, 30; 931-946.
Greco, P. (1960): "Recherches sur quelques formes d’inférences arithmétiques et sur la compréhension de l’itération numérique chez l’enfant". En J. Piaget (ed.), Problèmes de la construction du nombre. Paris: Presses Universitaires de France; pp. 149-213.
Greco, P. (1962): "Quantité et quotité". En P. Greco y A. Morf (eds.), Structures numériques élémentaires. Paris: Presses Universitaires de France; pp. 149-213.
Grize, J.B. (1979): “Observaciones sobre la epistemología matemática de los números naturales”. En J. Piaget (ed.), Tratado de lógica y conocimiento científico. Vol. II: Epistemología de la lógica. Buenos Aires: Paidós; pp. 109-120.
Guitel, G. (1975): Histoire comparée des numérations écrites. Paris: Flammarion.
Kingma, J. y Koops, W. (1981): “On the sequenciality of ordinality and cardinality”. International Journal of Behavioral Development, 4; 391-402.
Kingma, J. y Reuvekamp, J. (1984): “The construction of a developmental scale for seriation” . Educational and Psychological Measurement, 44; 1-23.
Lesh, R. y Doerr, H.M. (2003): Beyond Constructivism: Models and Modeling perspectives on Mathematics problem solving, learning, and teaching. Mahwah, NJ: Lawrence Erlbaum Associates.
Mareschal, D. y Shultz, T.R. (1999): “Development of children’s seriation: A connectionist approach”. Connection Science: Journal of Neural Computing, Artificial Intelligence and Cognitive Research, 11(2); 149-186.
Markman, E.M. (1978): “Empirical versus logical solutions to part-whole comparisons problems concerning classes and collections”. Child Development, 49(1); 168-177.
Markman, E.M. (1979): “Classes and collections: Conceptual organization and numerical abilities”. Cognitive Psychology, 11(4); 395-411.
Markman, E.M.; Horton, M.S. y McLanahan, A.G. (1980): “Classes and collections: Principles of organization in the learning of hierarchical relations”. Cognition, 8(3); 227-241.
Markman, E.M. y Seibert, J. (1976): “Classes and collections: Internal organization and resulting holistic properties”. Cognitive Psychology, 8(4); 561-577.
Mieville, D. (1985): “Connaissance et schematization”. Bulletin de Psychologie, 38(371); 625-630.
Piaget, J. (1977): Ensayo de lógica operatoria. Buenos Aires: Guadalupe (original en Paris: Dunod, 1971).
Piaget, J. e Inhelder, B. (1975): La génesis de las estructuras lógicas elementales. Clasificaciones y seriaciones. México: Guadalupe (original en Neuchâtel: Delachaux et Niestlé, 1959).
Piaget, J. y Szeminska, A. (1975): La génesis del número en el niño. México: Guadalupe (original en Neuchâtel: Delachaux et Niestlé, 1941).
Planche, P. (1998): “La construction des notions spatiales chez les enfants intellectuellement précoces ages de 6 à 8 ans”. Enfance, 2; 159-171.
Scholnick, E.; Nelson, K.; Gelman, S. y Miller, P. (eds.) (1999): Conceptual Development: Piaget’s Legacy. Mahwah, NJ: Lawrence Erlbaum Associates.
Serrano, J.M. (1980): Un modelo matemático para el aprendizaje de la conservación del número: Cadenas de Markov. Memoria de Licenciatura. Murcia: Universidad de Murcia.
Serrano, J.M. (1982): Un estudio de validación convergente para la determinación de niveles genéticos en la adquisición del concepto de número. Tesis doctoral. Murcia: Universidad de Murcia.
Serrano, J.M. (2005): Un modelo causal para la construcción del número: Implicaciones educativas. Murcia: D.M. Ed.
Serrano, J.M. y Denia, A.M. (1987): “Estrategias de conteo implicadas en los procesos de adición y sustracción”. Infancia y Aprendizaje, 39/40; 57-69.
Serrano, J.M. y Denia, A.M. (1994): ¿Cómo cuentan los niños?. Un análisis de las teorías más relevantes sobre la construcción de los esquemas de conteo. Murcia: Servicio de Publicaciones de la Universidad de Murcia.
Serrano, J.M. y Fernández, A. (1989): “Clases lógicas o colectivas?: ¿Dos modos de organización jerárquicas?”. Infancia y Aprendizaje, 38; 5-20.
Smith, L. (1999): “Necessary knowledge in number conservation”. Developmental Science, 2; 23-27.
Smith, L. (2002): Reasoning
by Mathematical Induction in Children’s Arithmetic. Amsterdam,
Sophian, (1995): “Representation and reasoning in early numerical development”. Child Development, 66; 559-567.
Van de Rijt, B.A.M. y Van Luit, J.E.H. (1999): “Milestones in the development of infant numeracy”. Scandinavian Journal of Psychology, 40(1); 65-71.